Derivative graph function draw given
Table of Contents
Table of Contents
If you’re studying calculus, you’ll eventually need to know how to draw the graph of a derivative. Derivatives are one of the core concepts in calculus, but they can be difficult to understand at first. In this blog post, we’ll explain how to draw the graph of a derivative so that you can master this important skill.
When it comes to derivatives, many people struggle with understanding the relationship between the original function and its derivative. The key to drawing the graph of a derivative is understanding that it shows the rate of change of the original function at any given point. Without this understanding, it can be challenging to accurately draw the graph of a derivative.
To draw the graph of a derivative, you’ll need to follow a few steps. First, you’ll need to identify the critical points of the original function. These are the points where the function is increasing, decreasing, or changing direction. Once you’ve identified these critical points, you can sketch the graph of the derivative by drawing a straight line through each point. The slope of this line will represent the rate of change of the original function at that point.
To summarize, to draw the graph of a derivative, you need to identify the critical points of the original function and sketch the derivative graph by drawing straight lines through each point. The slope of each line represents the rate of change of the original function at that point.
How to Draw the Graph of a Derivative: A Personal Experience
When I first started learning calculus, I struggled with drawing the graph of a derivative. It wasn’t until I took the time to understand the relationship between the original function and its derivative that I was able to accurately draw a derivative graph. One thing that helped me was practicing different problems until I felt confident in my ability. Once I had a good grasp of the concept, it was much easier to draw the graph of a derivative.
Understanding the Relationship Between Original Function and Derivative
The key to drawing the graph of a derivative is understanding the relationship between the original function and its derivative. The derivative shows the rate of change of the original function at any given point. If the original function is increasing, the derivative will be positive. If the original function is decreasing, the derivative will be negative. If the original function is at a maximum or minimum, the derivative will be zero.
When drawing the graph of a derivative, it’s important to remember that critical points on the original function will show up as either points where the derivative is zero or where the derivative is undefined.
Identifying Critical Points
One of the key steps in drawing the graph of a derivative is identifying the critical points of the original function. These are the points where the function is increasing, decreasing, or changing direction. At these points, the derivative will be zero or undefined.
Once you’ve identified the critical points, you can sketch the graph of the derivative by drawing straight lines through each point. The slope of each line will represent the rate of change of the original function at that point.
Practice Makes Perfect
If you’re really struggling with drawing the graph of a derivative, the best thing you can do is practice. Work through different problems until you feel confident in your ability to identify critical points and sketch the derivative graph accurately. With enough practice, you’ll master this important skill in no time.
Question and Answer
Q: How do I know if the derivative is positive or negative?
A: The derivative will be positive if the original function is increasing and negative if the original function is decreasing.
Q: How do I find the critical points of the original function?
A: Critical points are where the function is increasing, decreasing, or changing direction. At these points, the derivative will be zero or undefined.
Q: What is the slope of the derivative graph?
A: The slope of the derivative graph represents the rate of change of the original function at that point.
Q: Is it possible to have more than one critical point on a single graph?
A: Yes, it is possible to have multiple critical points on a single graph.
Conclusion of How to Draw the Graph of a Derivative
Drawing the graph of a derivative can be a challenging task, but with practice, anyone can master this important skill. Remember to identify the critical points of the original function, and sketch the derivative graph by drawing straight lines through each point. With enough practice, you’ll be able to accurately draw the graph of a derivative and understand the relationship between the original function and its derivative.
Gallery
How To Graph The Derivative Of A Function Given The Graph Of The
Photo Credit by: bing.com / graph derivative function original given antiderivatives quadratic equation reverse just ways main line sincerely helps hope idea topic
Draw The Function Given Graph Of Derivative - YouTube

Photo Credit by: bing.com / derivative graph function draw given
Derivative As Slope Of A Curve Derivative And Direction Of A Function

Photo Credit by: bing.com / derivative graphing slope curve calculus inference differentiation
Sketching Derivative Graphs At PaintingValley.com | Explore Collection
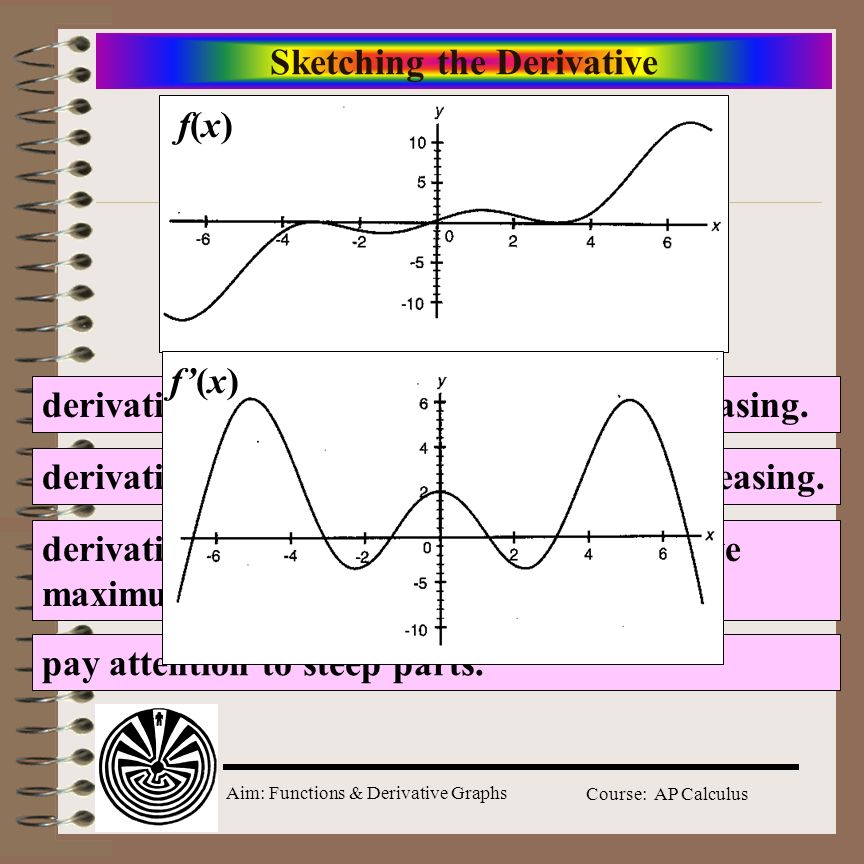
Photo Credit by: bing.com /
Derivative Graph Vs Original Function (w/ 15+ Examples!)
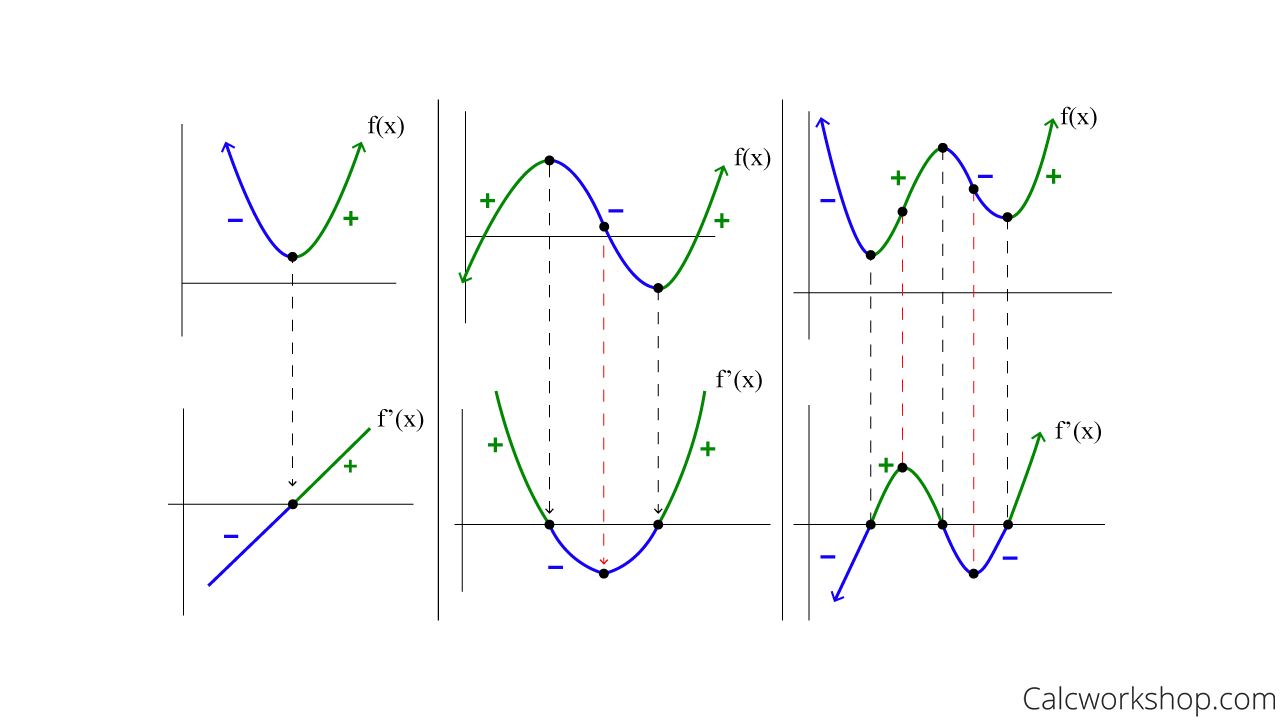
Photo Credit by: bing.com / derivative






